2.º Semestre de 2002

Professor: Marcus Vinícius A. Soares

Guilherme Augusto Sousa Guedes 03/36050

Daniel Farah 03/17870

Marcos Faustino 03/38745

Arthur Romano 03/33042

Reduzindo custos à toda prova

Nós, graduandos de Engenharia de Produção, fomos contratados pela Arisco. Esta empresa, afim de reduzir seus gastos, decidiu fabricar suas próprias embalagens.

Problema 1

Nossa primeira tarefa se inclui justamente nesse ponto, que é o de maximizar o volume da lata de extrato de tomate. No entanto, a Arisco compra da CSN (Companhia Siderúrgica Nacional) chapas de folha-de-flandres retangulares com o perímetro de 36cm. Os graduandos foram divididos em dois grupos, dos quais o nosso se incumbiu de determinar as dimensões ótimas da chapa que resultam no maior volume da lata.

Solução:

Antes de iniciarmos a resolução do problema, é conveniente desenharmos um diagrama da situação nos dada:

1) Inicialmente, nós encontramos a relação entre o perímetro e as dimensões x(comprimento) e y(largura) da chapa. Esta relação é dada por 2x+2y=36. Disso resulta que y=18-x. Considerando y=f(x), temos:
[> F:=x->18-x;

2) Após acharmos esta relação e levando em conta que o comprimento da circunferência, no caso representado por x, é igual a 2*Pi*R, encontramos a a seguinte relação:
[> R:=x->x/(2*Pi);

3) Como V= Pi*r^2*h e o raio e altura estão em função de x temos a seguinte função V(x):
[> V:=x->Pi*(R(x))^2*F(x); V(x);

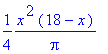
4) Ultilizando a ferramenta plot do Maple, esboçamos o gráfico da função V(x) e conseguimos o seguinte resultado:
[> plot(V(x),x=0..18);

5) Para visualizarmos melhor a função V(x) ultilizamos o expand :
[> R0 := expand(1/4/Pi*x^2*(18-x));

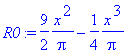
6) Uma vez descoberta a função, para achar o seu ponto máximo é necessário encontrar os seus números críticos. Para isso criamos uma função dV, que é igual a derivada de x.
[> dV:=unapply(diff(V(x),x),x); dV(x);

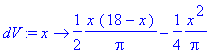
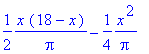
7) Para, preliminarmente, termos uma noção melhor de onde se localizam os números críticos de V(x), plotamos o gráfico de V(x), com x assumindo valores entre 0 e 18;
[> plot(dV(x),x=0..18);

8) Com o gráfico de dV(x), fica aparente que o volume é máximo quando x está próximo de 12. Depois, novamente ultilizamos o expand para visualizarmos melhor dV:
[> dVe := expand(1/2/Pi*x*(18-x)-1/4/Pi*x^2);

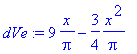
9) Agora que já obtemos a derivada da função V(x), para acharmos seus pontos críticos igualamos dV a zero:
[> solve(dV(x)=0,x);

10) Descobertos os pontos críticos determinamos qual dos dois é o máximo pelo simples cálculo de V(x) nesses pontos:
[> V(0);V(12);

11) A função V(x) assume seu valor máximo quando x=12. Falta determinarmos o valor de y. Para isso calculamos F(12):
[> F(12);

Fim do problema 1

Problema 2

Satisfeita com nosso desempenho, a Arisco nos designou mais um projeto. Em uma das etapas do processo de produção da massa de tomate, a polpa já processada é mantida em um recipiente cilíndrico. Para retirar completamente a polpa de dentro desse recipiente, pelo orifício inferior, são utilizadas duas pás acopladas a um eixo que corta o centro do cilindro. Para esvaziar completamente o recipente, a pá imediatamente ao lado do orifício é mantida fixa, enquanto a outra executa uma revolução completa no sentido anti-horário.

Seguindo a sua política de minimizar custos, a Arisco decidiu usar chapas de mesmo material utlizado nas latas, mantendo o mesmo perímetro de 36cm. A nossa tarefa é de calcular o maior volume do recipiente onde será guardada o polpa, tendo como base a chapa referida.

Inicialmente, reiniciamos todas as definições anteriores, exceto a que relaciona os lados x e y em relação ao perímetro. Novamente, é conveniente criar um esquema para melhor entendermos a questão:

Solução:
[> restart; F:=x->18-x;

1) Como no cilindro acima o raio corresponde ao valor x, e a altura, a F(x), definimos a função V(x) abaixo:
[> V:=x->Pi*x^2*F(x); V(x);

2) Para termos uma noção de como a função se comporta graficamente, plotamos-a a seguir
[> plot(V(x),x=0..18);

3) Parece-nos que o comportamento dessa função V é igual ao da função da tarefa anterior, inclusive com o seu valor maximo sendo atingido para x próximo de 12. Mas, para termos certeza disso, precisamos de criar, usando o unapply , uma função dV, sendo esta a derivada de V(x)
[> dV:=unapply(diff(V(x),x),x); dV(x);

4) Plotamos mais uma vez a função V(x), junto com sua derivada, para sabermos como estas se comportam:
[> plot({V(x),dV(x)},x=0..18);

5) Novamente, aqui expandimos a função dV, para que este fique mais clara
[> dVe := expand(2*Pi*x*(18-x)-Pi*x^2);

6) Agora, usando o comando solve , descobrimos para quais valores de x a derivada da função V(x) assume o valor zero.
[> solve(dV(x)=0,x);

7) Para sabermos qual dos números críticos corresponde ao de máximo, calculamos V(0) e V(12);
[> V(0);V(12);

8) Assim, descobrimos que o valor máximo do volume ocorre quando x é igual a 12. E, como a relação entre x e y é dada pela função F(x), calculamos F(12) para obtermos o valor de y:
[> F(12);

Surpreendentemente, as folhas-de-flandres, não importando com qual finalidade serão usadas, deverão ser do mesmo tamanho, fazendo com que a redução dos custos de produção na Arisco seja ainda maior.

Fim do problema 2