Cálculo I , Turma E , Prof.: Rui Siemetz

Projeto Laboratório 01

Identificação

Iona Teixeira Stevens - matr. : 03/20170

Fillippi Augusto Oliveira dos Santos - matr. : 03/35541

Ingrid Fernandes de Azevedo - matr. : 03/36530

Vanessa Ribeiro Soares - matr. : 03/41851

BORRACHAS PLEX

(Ex. 52 , Cálculo , G.B. Thomas )

Introdução

Joãozinho, aos dezenove anos de idade, após uma trágica morte de seus pais atacados por andorinhas famintas, herdou da família uma fabrica de borrachas para elásticos de aparelhos dentarios "Plex".

Ele, como todo bom filho, resolveu dar continuidade aquela linda tradição familiar. Porém, na primeira semana, percebeu que dirigir uma fabrica não era um lindo mundo como "SimCity" ou "Banco Imobiliário". Percebeu também que todas aquelas aulas de matemática, onde ele fazia sua siesta, faziam-lhe imensa falta neste momento.

Desesperado e preocupado com o futuro da grande linha "Plex", ele foi pedir ajuda ao seu grande mestre, o incomparável professor de matemática de terceiro grau, Lui. Este, sendo muito camarada, eternamente apaixonado pela matemática superior, aceitou a proposta do seu querido aluno.

Primeiro dia na fabrica : Enquanto Joãzinho brincava com o latex derretido, seu professor foi procurar o gerente, para analisar a situação da empresa, mais especificamente os custos de produção...

Não demorou para perceber que ninguém naquela fabrica prestava atenção aos custos de produção (descobriu-se posteriormente que o gerente era um picareta). Analisando os dados, Lui procurou minimizar o custo médio de produção de um lote de borrachas.

Suponha que c(x)= 2000 +96x +4x^(3/2), onde x representa milhares de unidades (um lote). Há um nível de produção que miniminize o custo médio? Em caso afirmativo, qual é?

Iniciando....
[> restart;

Desenvolvimento

Segundo dia na fabrica :

"João!!" Chamou Lui, "Pare com este videogame e venha aprender um pouco de admnistração de empresas". João, a contragosto, sentou-se em frente ao computador, numa tela de Maple e viu:
[> C:=x->2000+96*x+4*x^(3/2);

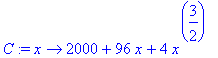
"Que que é isso, 'fessor'? "

" Isso é a função que define o custo de produção mensal de suas borrachas. Agora, mais importante que saber esse custo, é saber o Custo médio , ou seja, quanto a empresa gasta para produzir um lote de borrachas (milhares de unidades). Pelo o que eu pude ver, as indústrias "Plex" perderam uma enorme quantidade de dinheiro no semestre que passou, por isso é importante procurar minimizar o custo médio de produção".Custo médio: C(x)/x :
[> Cm:=x->(2000+96*x+4*x^(3/2))/x;

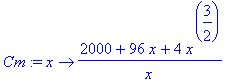
"E como se minimiza isso professor?"

"Primeiro tem que se calcular a derivada da função do custo médio, como você irá comandar esta empresa, você deve aprender bem a calcular a derivada no Maple". Joãzinho que não era tão tolo assim usou o comando Diff .
[> Diff(Cm(x),x)=diff(Cm(x),x);

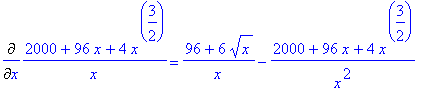
Agora definindo a derivada utilizando o comando unapply.
[> dCm:=unapply(diff(Cm(x),x),x);

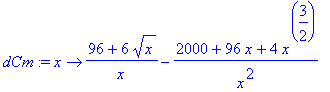
Vendo que Joãzinho parecia confuso em frente a tela, o professor explicou logo " Olha, isso vai servir para acharmos os pontos críticos, que indicarão a quantidade de lotes para o qual o custo médio é máximo ou mínimo...".... outro silencio.... "Você tem que igualar a derivada a zero, para achar esse(s) valor(es) mínimos ou máximos...". João lembrou que para resolver uma equação desse tipo no maple se usa o comando solve :
[> solve(dCm(x)=0,x);

"E como é que eu vou saber se esse número "100" corresponde ou máximo ou mínimo do custo médio de produção?"

"João, João, que decepção... Você não estudou nada não é? Você não lembra que agora se faz o teste da segunda derivada, para saber se a concavidade do gráfico de Cm é voltada para cima ( ou, seja, é o custo médio mínimo), ou para baixo ( seria então o custo médio máximo)."

A mente de João foi então iluminada : Ele lembrou que quando a derivada segunda num certo ponto é positiva, o valor corresponde ao valor mínimo, e se fosse negativa, ao valor máximo. Ele apressou-se para calcular a derivada segunda ...
[> Diff(dCm(x),x)=diff(dCm(x),x);

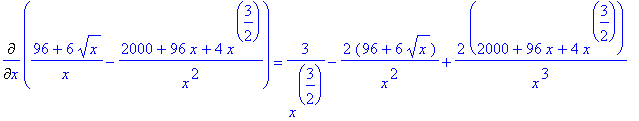
..., defini-la como sendo "d2Cm(x)"...
[> d2Cm:=unapply(diff(dCm(x),x),x);

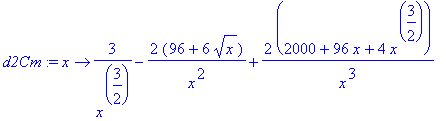
...e igualando a zero, usando os comandos solve e evalf :
[> evalf(solve(d2Cm(x)=0,x));

É positivo!!! A concavidade é pra cima...Joãozinho estava com o ego lá no alto, achava que sabia tudo sobre Maple, admnistração e Cálculo... pobre coitado....

Lui, sempre precavido, ao chegar em casa, resolveu verificar graficamente os resultados de Joãozinho ( ele queria ter certeza de que os cálculos de seu "aplicadíssimo" aluno estavam certos.)

Desenhou o gráfico do custo medio, para x entre 80 e 120, y entre 155.5 e 158 ...
[> plot([Cm(x)],x=80..120,y=155.5..158);

...e da derivada dCm , no intervalo x =(80,120)
[> plot([dCm(x)],x=80..120);

Conclusão

Lui verificou então, pelo gráfico, que o valor de custo médio mínimo, substituindo x por 100, era mesmo :
[> evalf(Cm(100));

Anos depois, aos 40 anos, Joãozão e suas derivadas eram os primeiros no mercado de exportação de latex.

Moral da história :

Matemático também fica rico!!