Alunos:
Fernanda H. Castro
Larissa R. R. Pereira
Pedro de C. Araújo
Uder M. de Assis
Ulisses Dias

Exercício 38

Uma rodovia Norte-Sul A e uma rodovia Leste-Oeste B se cruzam em um ponto P . Às 10:00 hs da manhã, passa por P um automóvel em direção norte a 80 Km/h. No mesmo instante, um avião voando em direção leste a 320 km/h a uma altitude de 8.800 metros passa por um ponto na rodovia B a 160 Km a oeste de P . Se o automóvel e o avião mantêm constantes suas velocidades e direções, em que instante eles estarão a uma distância mínima um do outro?

Pela figura temos indicado um tempo t qualquer após 10:00 Hs, em que x e y representam as distâncias percorridas pelo avião e pelo automóvel respectivamente, após t horas . d representa a distância entre o avião e o automóvel. z é a hipotenusa do triângulo retângulo formado pela altura do avião e pela distância y percorrida pelo automóvel após t horas. De acordo com a figura, podemos deduzir por relações trigonométricas:

> restart;

> 'd^2'=(x-160)^2 + z^2; 'z^2'=8.8^2 + y^2 ;

>

Podemos encontrar as distâncias x e y em função de suas velocidades :

> x:=t->320*t; y:=t->80*t;

>

Em que t corresponde a um tempo t qualquer (medido em horas) após 10:00hs. Substituindo x, y e z na equação e definindo d em função de t teremos:

> z:=t->(8.8^2 + y(t)^2)^(1/2);

> d:=t->((x(t)-160)^2 + z(t)^2)^(1/2); 'd(t)'=d(t);

>

Podemos fazer um gráfico da equação com tempo inicial ( t=0, e t medido em horas ) contado a partir de 10:00Hs.

> plot(d(t),t=-5..5,color=blue);

>

Para calcular os números críticos, obtemos a derivada da equação para descobrir onde ela é igual a 0.

> Diff(d(t),t)=diff(d(t),t);

>

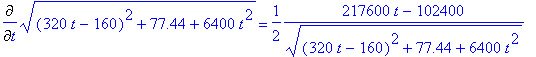
> dlinha:=t->diff(d(t),t);

>

> 'dlinha(t)'=dlinha(t);

>

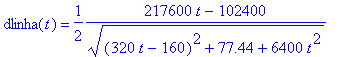
> solve(dlinha(t)=0,t);

>

De acordo com o comando SOLVE (em cima da derivada, para descobrir as raízes), isto ocorre quando t = 0.4705 h aproximadamente. Podemos verificar isto graficamente:

> plot(d(t),t=0.4..0.5,color=blue);plot({d(t),dlinha(t)},t=0..2,color=[red,blue]);

>

>

O grafico vermelho representa a derivada da função d(t) e o azul a distância em função do tempo (a função d(t)).

Calculando, podemos descobrir exatamente o instante. Basta adicionar .4705 de hora à 10:00Hs , o que corresponde a:

Resposta: 10 Hs 28 Min 14.11764708 segundos