S é a superfície de nível, no nível k = 18,
da função
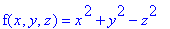
Assim, como no caso bidimensional, o vetor gradiente
grad f(x, y, z) é ortogonal a S no ponto (x, y, z). Em particular, grad f(
![P[0]](images/th2_11_5_286.gif) ) é um vetor ortogonal a S no ponto
) é um vetor ortogonal a S no ponto ![P[0]](images/th2_11_5_287.gif) . Calculando, obtém-se que grad f(x, y, z) = (2x, 2y, -2z),
e portanto grad f(
. Calculando, obtém-se que grad f(x, y, z) = (2x, 2y, -2z),
e portanto grad f( ![P[0]](images/th2_11_5_288.gif) ) = (6, 10, 8). Dessas observações segue-se que:
) = (6, 10, 8). Dessas observações segue-se que:
a) o plano tangente a S no ponto ![P[0]](images/th2_11_5_289.gif) é aquele que passa por esse ponto e é ortogonal a grad
f(
é aquele que passa por esse ponto e é ortogonal a grad
f( ![P[0]](images/th2_11_5_2810.gif) ). Logo, para um ponto genérico P = (x, y, z), esse plano
tem equação < grad f(
). Logo, para um ponto genérico P = (x, y, z), esse plano
tem equação < grad f( ![P[0]](images/th2_11_5_2811.gif) ), P -
), P - ![P[0]](images/th2_11_5_2812.gif) > = 0. Substituindo os valores, obtém-se que a equação
do plano é
> = 0. Substituindo os valores, obtém-se que a equação
do plano é
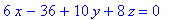
b) a reta normal a S em ![P[0]](images/th2_11_5_2814.gif) é aquela que passa por esse ponto e tem a mesma direção
de grad f(
é aquela que passa por esse ponto e tem a mesma direção
de grad f(![P[0]](images/th2_11_5_2815.gif) ).
Logo, essa reta tem equação P(t) =
).
Logo, essa reta tem equação P(t) = ![P[0]](images/th2_11_5_2816.gif) + t grad f(
+ t grad f( ![P[0]](images/th2_11_5_2817.gif) ). Substituindo os valores, obtém-se que a equação da reta
é
). Substituindo os valores, obtém-se que a equação da reta
é
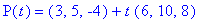
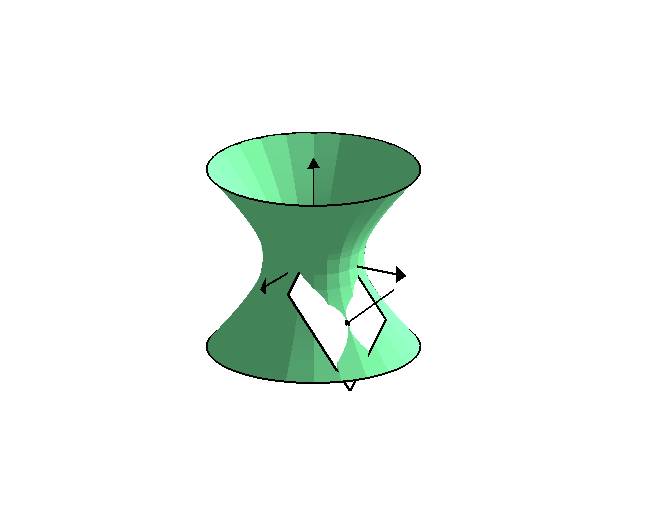
A figura abaixo ilustra a superfície S juntamente
com o ponto ![P[0]](images/th2_11_5_2819.gif) , o plano tangente e a reta normal.
, o plano tangente e a reta normal.


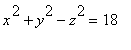 e o ponto
e o ponto
