| |
 |
Thomas 11ed , Capítulo
15 , Seção
15.4 , Exercício
32
|
 |
Índice
do Banco de Exercícios de Cálculo 3
->
Integrais triplas em coordenadas cartesianas |
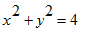 pelos planos
pelos planos
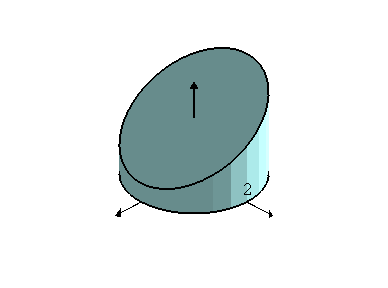
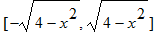 . Daí segue-se que
. Daí segue-se que